我们已经掌握了如何把三维投影到二维屏幕,那么如何把点绘制到屏幕上呢?这个过程称为光栅化(Rasterization)。
对于现代显示设备,把一块显示区域划分了许多更小的基本单位区域,称为像素(Pixel)。每个像素都有对应的索引(Pxiels’ indeces):
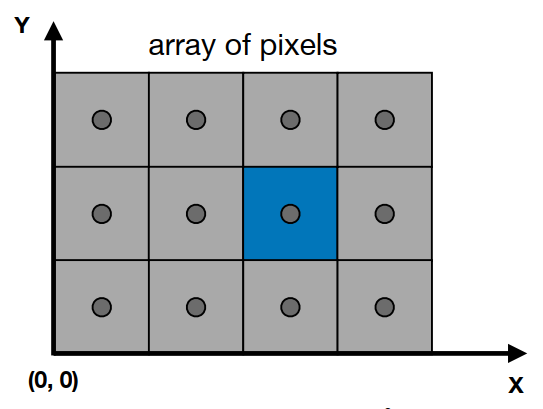
像素索引到屏幕空间坐标有 \((x,y) \rightarrow (x+0.5,y+0.5)\)
三角面(Triangle Meshes)
三维空间中,最少3个点构成一个平面。因此,所有的三维物体均可以通过三角面微分。
光栅采样(Rasterization As 2D Sampling)
那么,把一个三维模型绘制到二维平面上,等同于把一个三维空间内的三角面绘制到二维平面上。通过MVP和Viewport变换,我们可以得到三角面在屏幕上的坐标,如下图。
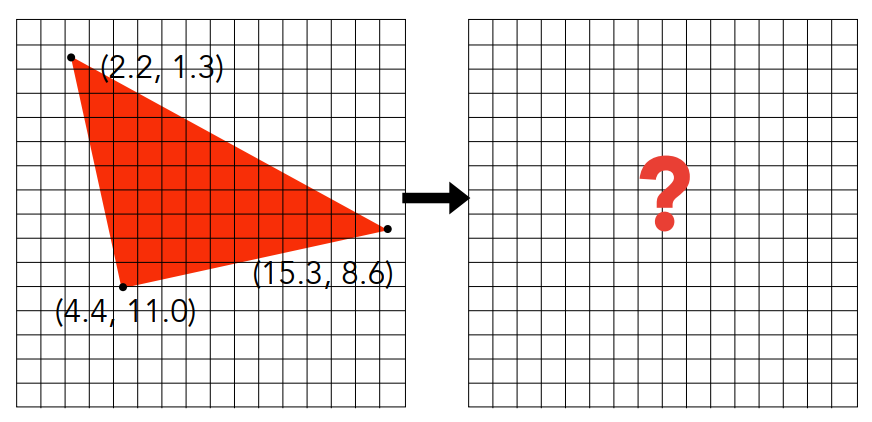
接下来只要把坐标对应的像素填充,就可以画出这个三角面。
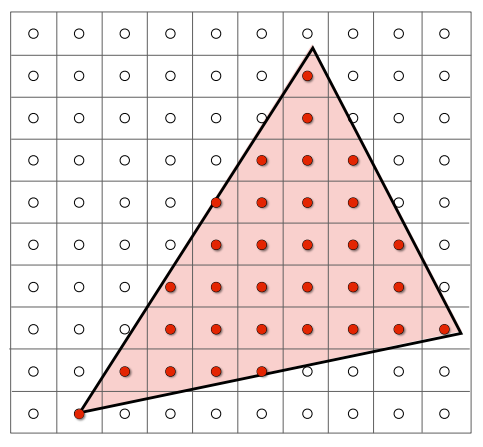
这个时候,我们会遇到一个问题:
知道三角面三个点的坐标,但是这三个点围成的区域的点怎么办呢?
答:找出所有在三角形内的点。
Evaluating inside(tri, x, y)
我们如何判断一点 \(Q\),是否在由 \(P_0,P_1,P_2\) 组成的三角形内呢?
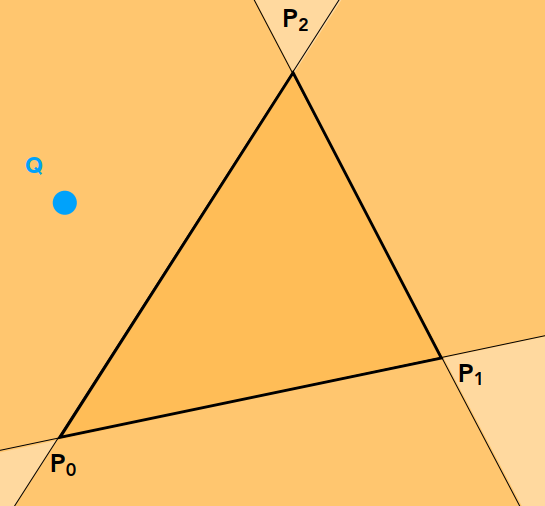
由 GAMES101:线性代数之向量 我们可以通过分别计算 \(QP_0 \times P_1 P_0, QP_1 \times P_2 P_1, QP_2 \times P_0 P_2\) ,若三个叉乘的值方向相同(二维向量正负表示方向),则 \(Q\) 在 \(P_0,P_1,P_2\) 组成的三角形内。(注:区域顶点按逆时针或顺时针排列)
有了判定方法,但是Q点可以是屏幕上的任意一点,遍历去做那可太顶了,得想个快速的办法:只计算在三角面包围核(Bounding Box)内的点。
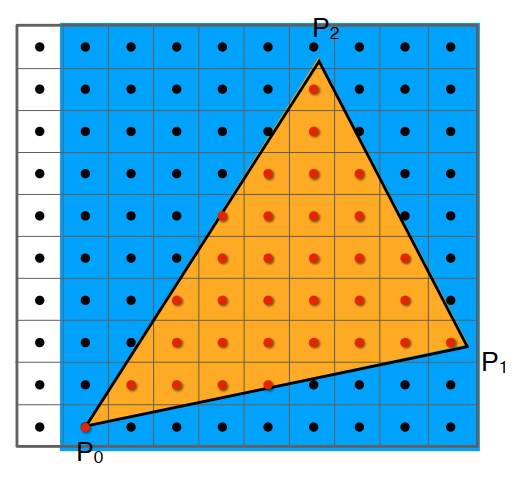
上述方法遇到长条的三角面,包围核会变的很大。当然还有更快更好的方式:通过顶点,向一方向的相邻点进行检测,若在三角面内,则继续当前方向;若不在,则改变方向。
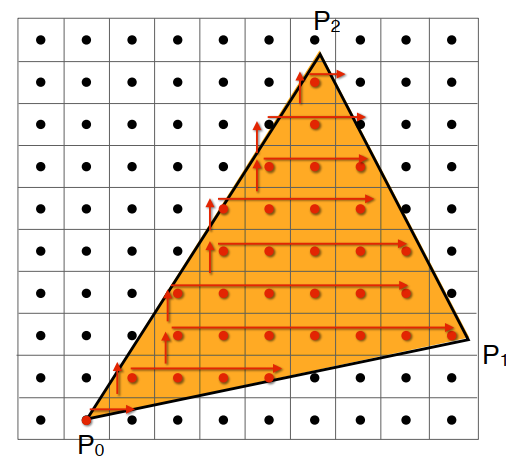
终于我们画出了一个三角面的二维图像!
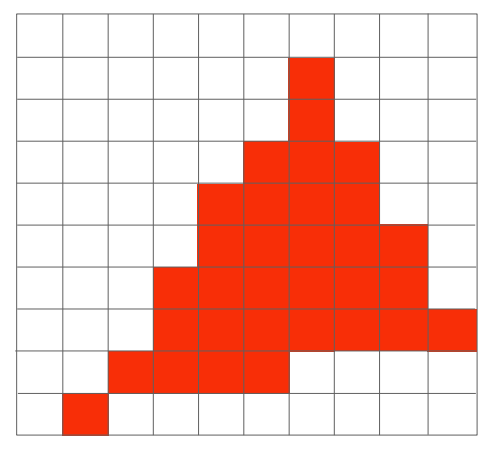
小结
我们得到了最终的图像,但是也发现了几个问题:
如果点Q,既在Tri1边缘上,也在Tri2边缘上,
我们该怎么裁决呢?
由于像素索引坐标都是整数,Q是离散的,
得到的图案并不光滑,存在很多锯齿(Jaggies)。
关于上述锯齿问题可以认为是采样精度问题,可以通过把一像素进一步拆分采样,求平均得到平滑的边缘(MSAA Supersampling)
