向量（Vectors）

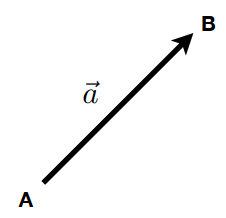
定义向量有 \(\vec{a}=\vec{AB}=B-A\)，几何意义如上图所示。

一个向量表示2个点的相对关系，可表示其方向和大小 \(\|\vec{AB}\|\)，常见二维 \((x, y)\)，三维 \((x, y, z)\)。另一类常用向量，单位向量：\(\vec{a}/\|\vec{a}\|\)，即长度为1的向量。

计算，\(\vec{AB}=(B_x, B_y, B_z)-(A_x, A_y, A_z)=(B_x-A_x, B_y-A_y, B_z-A_z) \\ \|\vec{a}\|=\sqrt{x^2+y^2+z^2}\)

向量的计算

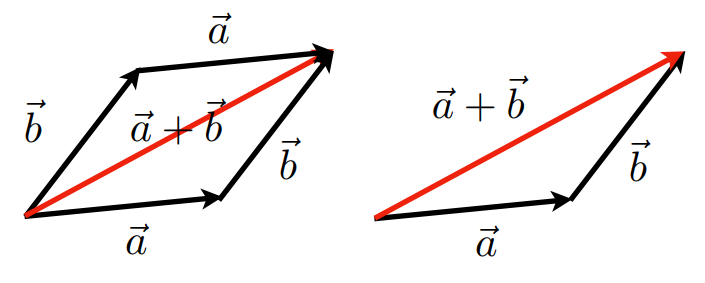
如上图，展示了\(\vec{a}+\vec{b}\)的平行四边形法则和三角形法则。简单来说，将一组相加的向量逐个尾首相连，第一个向量的首与最后一个向量的尾的向量，即结果。向量加减法满足交换律、结合律。

计算：\(\vec{a}+\vec{b}=(x_a, y_a, z_a)+(x_b, y_b, z_b)=(x_a+x_b, y_a+y_b, z_a+z_b)\)，直接将其维度上的值相加。

向量的点乘（Dot Product）

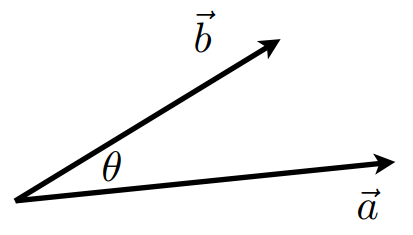
对于两个向量，定义他们的点乘为：\(\vec{a}\cdot\vec{b}=\|\vec{a}\|\|\vec{b}\|\cos\theta\)，即向量的长度的乘积乘其夹角的余弦值。向量点乘满足交换律、分配律。

由此我们也可以很快的得到计算2个向量的夹角：\(\cos\theta = \frac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|\|\vec{b}\|}\)。

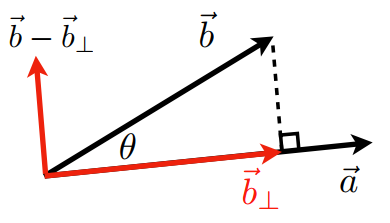
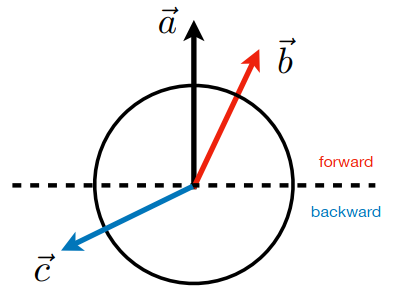
进一步，\(\frac{\vec{a}\cdot\vec{b}}{\|\vec{a}\|}\) 则表示 \(\vec{b}\) 在 \(\vec{a}\) 方向上的投影长度。

向量的点乘，通常我们用于求解向量间的夹角、向量的拆分、判别2个向量同向（forward，dot>0）或背离（backward，dot<0）。

计算：\((x_a, y_a, z_a)\cdot(x_b, y_b, z_b)=(x_a x_b, y_a y_b, z_a z_b)\)，直接将其维度上的值相乘。

向量的叉乘（Cross Product）

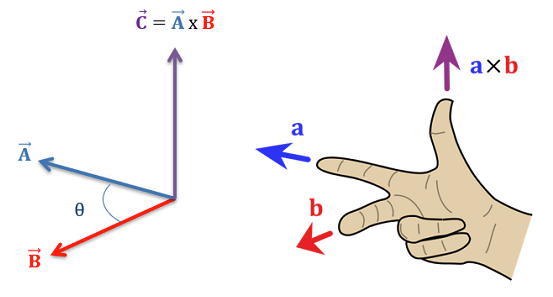
几何意义如上图，我们定义 \(\vec{C}=\vec{A}\times\vec{B}=-\vec{B}\times\vec{A}\)。\(\vec{C}\) 为2向量的叉乘，其方向与 \(\vec{A}\) 和 \(\vec{B}\) 垂直，其大小为 \(\|\vec{A}\times\vec{B}\|=\|\vec{A}\|\|\vec{B}\|\sin\theta\)。

向量的叉乘，常用于求平面的法线、求某朝向下的标准轴、判断点是否在三角形内/外（对于后面进行光栅化（Rasterization）有很大的作用）。

接下来我们进行计算推导：

定义基向量\(\vec{x} \vec{y} \vec{z}\)。（即3维坐标下的3个轴）

根据叉乘定义：\(\vec{x}\times\vec{y}=\vec{z}\\ \vec{y}\times\vec{z}=\vec{x}\\ \vec{z}\times\vec{x}=\vec{y}\\ \vec{x}\times\vec{x}=\vec{y}\times\vec{y}=\vec{z}\times\vec{z}=\vec{0}\)

根据反交换律：\(\vec{y}\times\vec{x}=-\vec{z}\\ \vec{z}\times\vec{y}=-\vec{x}\\ \vec{x}\times\vec{z}=-\vec{y}\)

定义 \(\vec{A}=a\vec{x}+b\vec{y}+c\vec{z}, \vec{A}=(a,b,c)\)

定义 \(\vec{B}=e\vec{x}+f\vec{y}+g\vec{z}, \vec{B}=(e,f,g)\)

\( \begin{align}\vec{A}\times\vec{B}=&(a\vec{x}+b\vec{y}+c\vec{z})\times(e\vec{x}+f\vec{y}+g\vec{z}) \\=&ae(\vec{x}\times\vec{x})+af(\vec{x}\times\vec{y})+ag(\vec{x}\times\vec{z}) \\&+be(\vec{y}\times\vec{x})+bf(\vec{y}\times\vec{y})+bg(\vec{y}\times\vec{z}) \\&+ce(\vec{z}\times\vec{x})+cf(\vec{z}\times\vec{y})+cg(\vec{z}\times\vec{z}) \\=&ae(\vec{0})+af(\vec{z})-ag(\vec{y}) \\&-be(\vec{z})+bf(\vec{0})+bg(\vec{x}) \\&+ce(\vec{y})-cf(\vec{x})+cg(\vec{0}) \\=&(bg-cf)\vec{x}+(ce-ag)\vec{y}+(af-be)\vec{z} \end{align} \)

最后有 \(\vec{A}\times\vec{B}=(bg-cf, ce-ag, af-be)\)

小结

在Unity中，使用左手坐标系，左手法则判断朝向。