变换（Transformation）

想象一块画布，我们可以在画布上绘制一个图案。通常我们会对图像进行位移、旋转、放大缩小的操作，这些操作称为2D变换（2D Transformations）。

同样的，在空间中，我们对一个物体也可以进行位移（Translation）、旋转（Rotation）、缩放（Scale），称这些操作为3D变换（3D Transformations）。

那么我们进一步思考，相机拍摄出的照片是2D的，但是对象却是3D的。没错，实现三维空间到二维空间的变换，就可以把物体渲染成图片了。

缩放（Scale）

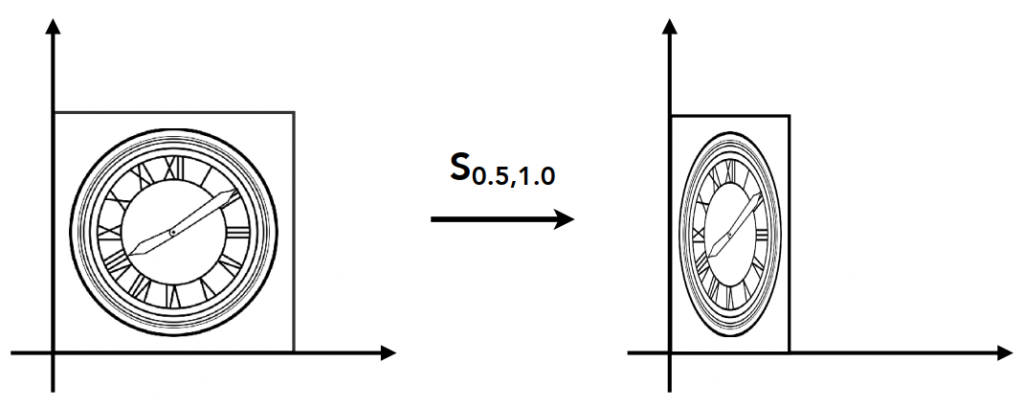
如图，将左图水平缩小到原来的0.5倍，垂直方向不变。

坐标变换：\(x’=s_{x} x \\ y’=s_{y} y\)。

写成矩阵形式：\(\begin{pmatrix} x’ \\ y’ \end{pmatrix} =\begin{pmatrix} s_{x} & 0 \\ 0 & s_{y} \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} \)

若变换矩阵形如 \(\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}\)（Reflection Matrix），则可实现翻转变换，如下图。

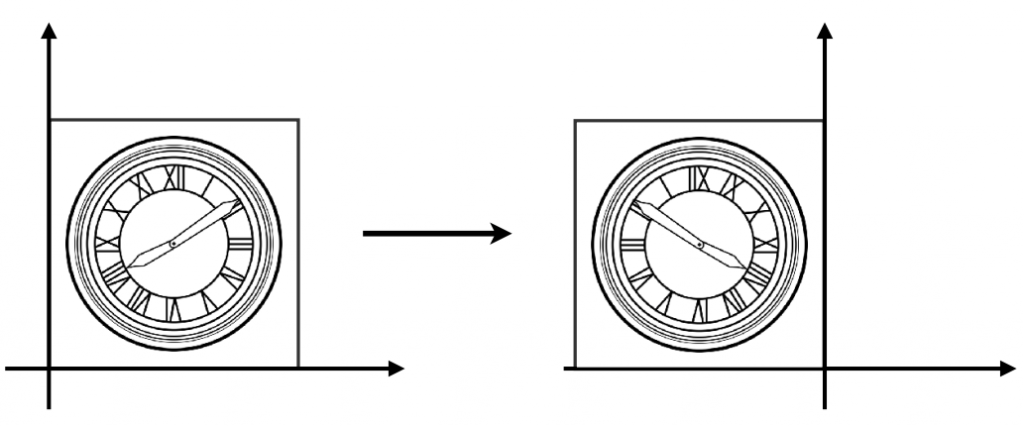
若变换矩阵形如 \(\begin{pmatrix} 1 & a \\ b & 1 \end{pmatrix}\)（Shear Matrix），则可实现错切变换，如下图。

当 \(a=1, b=0\) 时，为水平移位。当 \(a=0, b=1\) 时，为垂直移位。

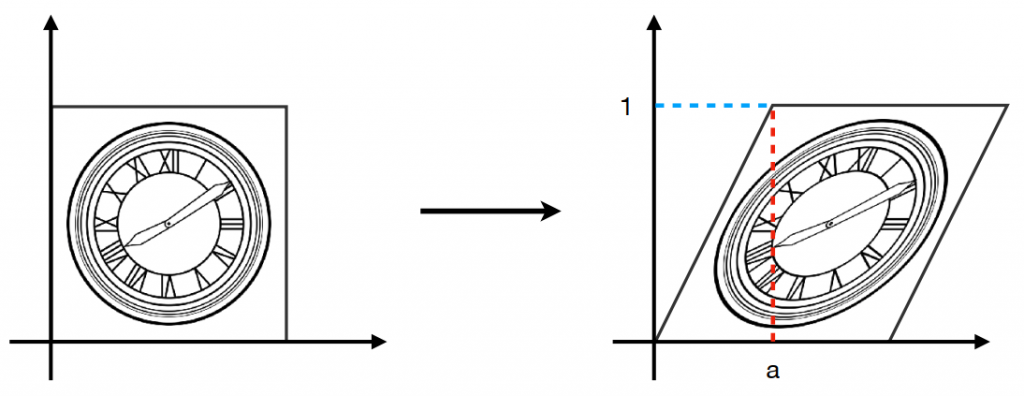
旋转（Rotation）

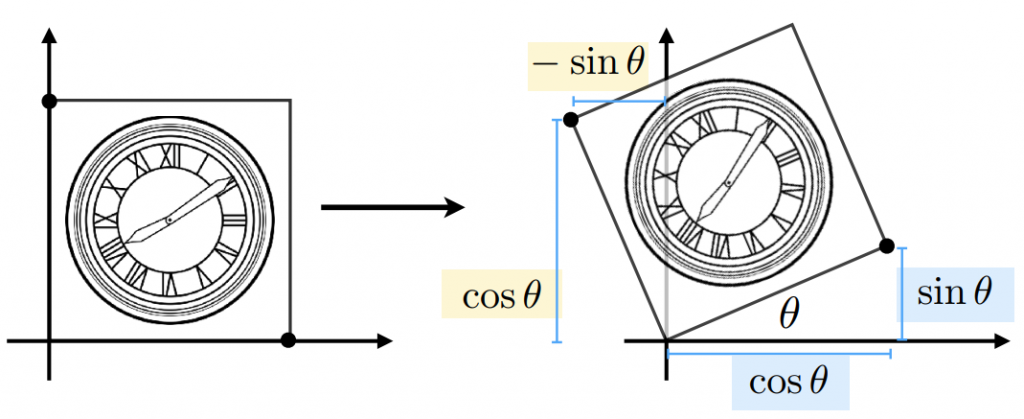
若将图像各个坐标绕原点逆时针旋转\(\theta\)度，有变换矩阵 \(R_{\theta}=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}\)（Rotation Matrix）

位移（Translation）

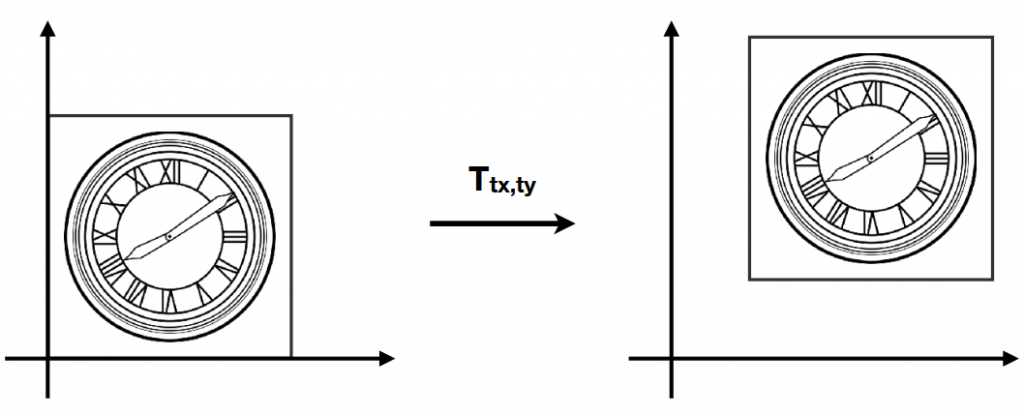
坐标变换：\(x’=x+t_{x} \\ y’=y+t_{y}\)。

矩阵形式：\(\begin{pmatrix} x’ \\ y’ \end{pmatrix} =\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} +\begin{pmatrix} t_{x} \\ t_{y} \end{pmatrix}, \begin{cases}a=d=1\\b=c=0\end{cases} \)

注意到，位移变换（仿射变换 Affine transformation）和缩放、旋转的矩阵形式不一样…那么，能不能把三者统一成一种形式，通过矩阵乘法将其进行组合呢？

齐次坐标（Homogenous Coordinates）

通过对一组坐标添加一个额外维度坐标w，对于点有w=1，向量有w=0。齐次坐标 \(\begin{pmatrix}x\\y\\w\end{pmatrix}\) 为点，满足 \(\begin{pmatrix}\frac{x}{w}\\\frac{y}{w}\\1\end{pmatrix}, w \ne 0\)

变换矩阵可以写成 \(\begin{pmatrix} x’ \\ y’ \\ 1 \end{pmatrix} =\begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1\end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix}ax+by+t_x \\ cx+dy+t_y \\ 1 \end{pmatrix} \)

逆变换（Inverse Transform）

我们有变换 \(\begin{pmatrix} x’ \\ y’ \\ 1 \end{pmatrix} = A \begin{pmatrix}x \\ y \\ 1 \end{pmatrix} \)

则 \(\begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = B\begin{pmatrix}x’ \\ y’ \\ 1 \end{pmatrix} \) 称 \(B\) 为 \(A\) 的逆变换，\(B=A^{-1}\)

组合变换（Composing Transforms）

通过齐次坐标，统一了三种变换的矩阵形式。因此，我们可以通过矩阵的乘法（按顺序左乘，即从右边向左计算乘法）对变换进行组合。注意：矩阵乘法不满足交换律。

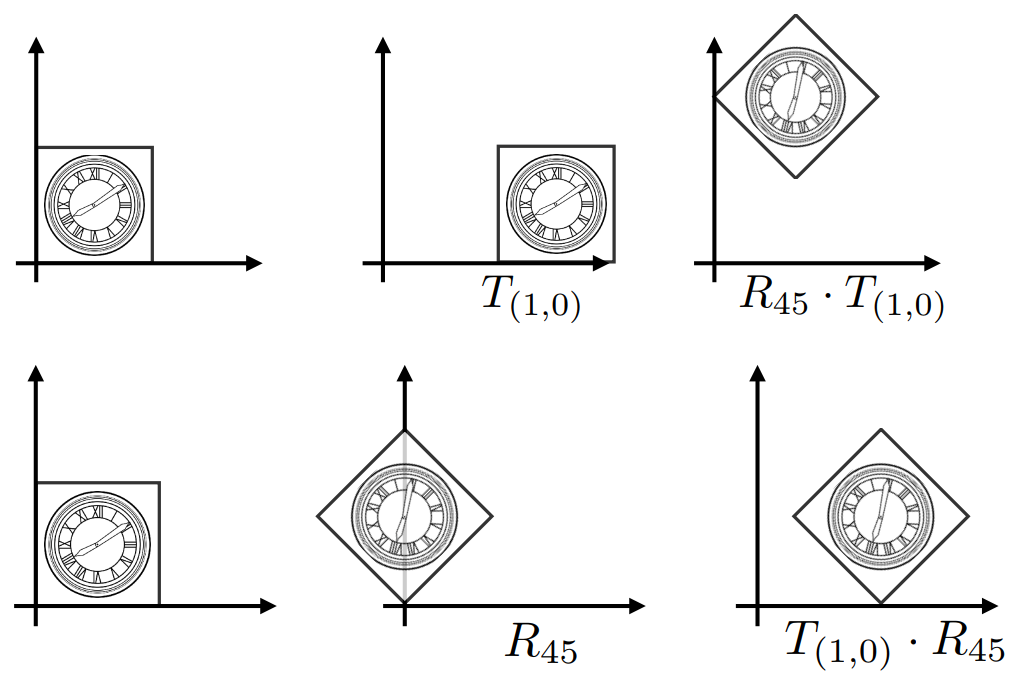
\(R_{45}T_{(1,0)} \ne T_{(1,0)}R_{45}\)，上图以可视化的方式展示了变换的不可交换性。

先逆时针旋转45度，再位移（1，0）写为 \(T_{(1,0)}R_{45}\begin{pmatrix}x\\y\\1\end{pmatrix} = \begin{pmatrix}1 & 0 & 1\\0 & 1 & 0\\0 & 0 & 1\end{pmatrix}\begin{pmatrix}\cos45^\circ & -\sin45^\circ & 0\\\sin45^\circ & \cos45^\circ & 0\\0 & 0 & 1\end{pmatrix}\begin{pmatrix}x\\y\\1\end{pmatrix}\)

三维变换（3D Transformations）

通过对一组坐标添加一个额外维度坐标w，对于点有w=1，向量有w=0，转换为齐次坐标。齐次坐标 \(\begin{pmatrix}x\\y\\z\\w\end{pmatrix}\) 为点，满足 \(\begin{pmatrix}\frac{x}{w}\\\frac{y}{w}\\\frac{z}{w}\\1\end{pmatrix}, w \ne 0\)

变换矩阵可以写成 \(\begin{pmatrix} x’ \\ y’ \\ z’ \\ 1 \end{pmatrix} =\begin{pmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z\\ 0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} \)

3D – 缩放变换

\(S_{(s_x,s_y,s_z)} = \begin{pmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)

3D – 位移变换

\(T_{(t_x,t_y,t_z)} = \begin{pmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{pmatrix}\)

3D – 旋转变换

绕X轴旋转 \(R_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\alpha & -\sin\alpha & 0 \\ 0 & \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)

绕Y轴旋转 \(R_y(\alpha) = \begin{pmatrix} \cos\alpha & 0 & \sin\alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin\alpha & 0 & \cos\alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)

绕Z轴旋转 \(R_z(\alpha) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 & 0 \\ \sin\alpha & \cos\alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\)

在三维空间中，我们通常用一组欧拉角\((\alpha,\beta,\theta)\)表示物体绕xyz三个轴的旋转角。由于变换的不可交换性，每个轴旋转变换的应用顺序不同，最后的效果也不一样。\(R_{xyz}(\alpha,\beta,\theta) = R_x(\alpha)R_y(\beta)R_z(\theta)\)

小结

What’s the order?
Linear Transform first or Translation first?

关于上述的顺序问题，由于Rotation的操作表示绕原点进行旋转，应当先进行线性变换（Scale、Rotate）再进行Translation位移操作。

在Unity中，3D物体的欧拉角旋转变换的顺序为 \(R_{zxy}(\theta,\alpha,\beta) = R_z(\theta)R_x(\alpha)R_y(\beta)\)